√99以上 partial derivative of 1/(x^2 y^2 z^2) 129344-Partial derivative of 1/sqrt(x^2+y^2+z^2)

Partial derivative of x1/2 y \frac{\partial}{\partial x}(x\frac{1}{2}y) ar Related Symbolab blog posts Practice Makes Perfect Learning math takes practice, lots of practice Just like running, it takes practice and dedication If you want In order to calculate the tangent plane at P = (3, 4, 5), we can consider the parametrization φ(x, y) = (x, y, √50 − x2 − y2) Consequently, the tangent plane π at the given point can be described by (x, y, z) = P αφx(3, 4) βφy(3, 4) where (α, β) ∈ R2 Share edited Jan 4 '19 at 026 answered Jan 3 '19 at 2142 user0102Hint type x^2,y to calculate `(partial^3 f)/(partial x^2 partial y)`, or enter x,y^2,x to find `(partial^4 f)/(partial x partial y^2 partial x)` If the calculator did not compute something or you have identified an error, or you have a suggestion/feedback, please write it in the comments below

Se13e01 01 Gif

Partial derivative of 1/sqrt(x^2+y^2+z^2)

Partial derivative of 1/sqrt(x^2+y^2+z^2)-(i) y =x2 2xz z2 x z x y =2 2 ∂ ∂ 2 2 2 = ∂ ∂ x y 2 2 = ∂ ∂ ∂ x z y x z z y =2 2 ∂ ∂ 2 2 2 = ∂ ∂ z y 2 2 = ∂∂ ∂ z x y (ii) y =x2 z2 3z 2xz2 x y = ∂ ∂ 2 2 2 2z x y = ∂ ∂ xz x z y 4 2 = ∂ ∂ ∂ =2 2 3 ∂ ∂ x z z y 2 2 2 2x z y = ∂ ∂ xz z x y 4 2 = ∂∂ ∂ (iii) = =xz−1 z x y z z x y 1 1 = = ∂ ∂ − 0 2 2 = ∂ ∂ x y 2 2 2 1 z z x z y =− =− ∂ ∂ ∂ − 2 2 z x xz z y =− =− ∂ ∂ − 3 3 2 2 2 2 z x xz z y = = ∂ ∂EXAMPLE 1415 Suppose the temperature at (x,y,z) is T(x,y,z) = e−(x2y2z2) This function has a maximum value of 1 at the origin, and tends to 0 in all directions If k is positive and at most 1, the set of points for which T(x,y,z) = k is those points satisfying x 2y2 z = −lnk, a sphere centered at the origin The level surfaces are the

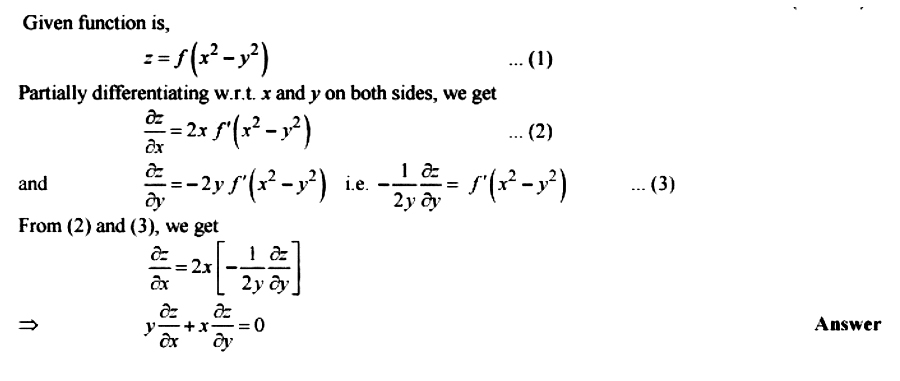
Form A Partial Differential Equation By Eliminating Arbitrary Function From Z F X 2 Y 2 Mathematics 2 Question Answer Collection

But by alternately setting x=1 (red), x=05 (white), and x=025 (green), we can take slices of z=x 2y 2 (each one a plane parallel to the zy plane) and see different partial functions We can get a further idea of the behavior of the function by considering that the same curves are obtained for x=1, 05 and 025Introduction Suppose that f is a function of more than one variable For instance, z = f ( x , y ) = x 2 x y y 2 {\displaystyle z=f (x,y)=x^ {2}xyy^ {2}} A graph of z = x2 xy y2 For the partial derivative at (1, 1) that leaves y constant, the corresponding tangent line is parallel to the xz@x@y means difierentiate flrst with respect to y and then with respect to x The \mixed" partial derivative @ 2z @x@y is as important in applications as the others It is a general result that @2z @x@y = @2z @y@x ie you get the same answer whichever order the difierentiation is done 08 Example Let z = 4x2 ¡ 8xy4 7y5 ¡ 3 Find all the flrst and second order partial derivatives

Then the x2 y2 z z tangent plane is z = z0 0 x0 (x−x y0 x0 x y0 y , since x2y2 = z2 0) (y−y0), or z =Definition 1331 Partial Derivative Let z = f(x, y) be a continuous function on an open set S in ℝ2 1 The partial derivative of f with respect to x is fx(x, y) = lim h → 0f(x h, y) f(x, y) h 2 The partial derivative of f with respect to y is fy(x, y) = lim h → 0f(x, y h) f(x, y) h † † marginUse the limit definition of partial derivatives to calculate ∂ f/ ∂ x for the function f(x, y, z) = x2 − 3xy 2y2 − 4xz 5yz2 − 12x 4y − 3z Then, find ∂ f/ ∂ y and ∂ f/ ∂ z by setting the other two variables constant and differentiating accordingly Solution

If u = f (x,y) 2 then, partial derivative of u with respect to x and y defined as u x = n f ( x, y) n – 1 u_ {x} = n\left f\left ( x,y \right ) \right ^ {n – 1} ux = nf (x,y)n–1 ∂ f ∂ x \frac {\partial f} {\partial x} ∂x∂fPartial Derivative Formulas and Identities There are some identities for partial derivatives as per the definition of the function 1 If u = f (x,y) and both x and y are differentiable of t ie x = g (t) and y = h (t), then the term differentiation becomes total differentiation 2X, f y and f z The partial derivative is calculate d by holding y and z constant Likewise, for and 212 Partial Derivative as a Slope Example 26 Find the slope of the line that is parallel to the xzplane and tangent to the surface z x at the point x Py(1, 3, 2) Solution Given f x y x x y( , ) WANT (1,3) f x

Partial Fractions Calculator Wolfram Alpha

14 Partial Derivatives Copyright Cengage Learning All Rights

 \\frac{{\partial w}}{{\partial y}} = {x^2} y{z^3} 28{\sec ^2}\left( {4y} \right)\ Finally, let's get the derivative with respect to \(z\) Since only one of the terms involve \(z\)'s this will be the only nonzero term in the derivative Also, the \(y\)'s in that term will be treated as multiplicative constantsDerivatives calculated as if x, y, z were independent ∂w Example 2 Find , where w = x3y −z2t and xy = zt ∂y x,t Solution 1 Using the chain rule and the two equations in the problem, we have ∂w ∂z x = x 3 −2zt = x 3 −2zt = x 3 −2zx ∂y x,t ∂y x,t t Solution 2Free partial derivative calculator partial differentiation solver stepbystep

Doc Chapter Four Derivatives Of Multivariate Functions Partial Differentiation Habtamu Destaw Academia Edu

1

1 If z = f(x,y) = x4y3 8x2y y4 5x, then the partial derivatives are ∂z ∂x = 4x3y3 16xy 5 (Note y fixed, x independent variable, z dependent variable) When we are taking a partial derivative all variables are treated as fixed constant except two, the independent variable and the dependent variable2 PARTIAL DIFFERENTIATION 1 b) wx = −y2/x2, wy = 2y/x;Example 2 Find ∂z ∂x and ∂z ∂y for the function z = x2y3 Solution z = x2y3 ∴ ∂z ∂x = 2xy3, and ∂z ∂y = x23y2, = 3x2y2 For the first part y3 is treated as a constant and the derivative of x2 with respect to x is 2x For the second part x2 is treated as a constant and the derivative of y3 with respect to is 3 2 Exercise 1

Http Abel Math Harvard Edu Archive 21a Fall 09 Resources Chapter11 Supp Pdf

Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch15 Pdf

The plane x = 1 intersects the paraboloid z = x2 y2 in a parabola Find the slope of the tangent to the parabola at (1;2;5) The tangent to the curve of intersection of the plane x = 1 and surface z = x2 y2 at the point (1;2;5) P Sam Johnson Partial Derivatives 18/117 We have, as you write correctly, $$ \def\p#1#2#3{\frac{\partial^{#3} #2}{\partial #1^{#3}}}\p x{}{} f(r) = f'(r)\p x r{} $$ Taking another derivative, we have, using the product rule first $$ \p x{}2 f(r) = \p x{}{}\left(f'(r) \p xr{}\right) = \p x{}{} f'(r) \p xr{} f'(r) \p xr2$$ Using the chain rule in the first term as for the first derivative, gives $$ \p x{}2 f(r) = f''(r) \left(\p xr{}\right)^2 f'(r)\p xr2 $$ Now, $$ \p xr{} = \frac xr, \quad \p xr2 = \frac{r \frac{x^2}r}{r^2So let's say I have some multi variable function like f of XY so they'll have a two variable input is equal to I don't know x squared times y plus sine of Y so a lot of put just a single number it's a scalar valued function question is how do we take the derivative of an expression like this and there's a certain method called a partial derivative which is very similar to ordinary derivatives

F X Y X 2 Y Y Y F F X X 2xyx 2 3y Y Ln2 Z F X Y Cos Xy X Cos 2

Practice Problems 10 And 11

 Explanation Since you're dealing with a multivariable function, you must treat x, y, and z as independent variables and calculate the partial derivative of w, your dependent variable, with respect to x, y, and z When you differentiate with respect to x, you treat y and z as constants LIkewise, when you differentiate with respect to y, you treatFor a two variable function f(x , y), we can define 4 second order partial derivatives along with their notations Examples with Detailed Solutions on Second Order Partial Derivatives Example 1 Find f xx, f yy given that f (∂ x 3 y 4 x 2 y / ∂x) / ∂x = ∂( 3 x 2 y 4 2 x y) / ∂x = 6x y 4 2y f yy is calculated as follows f yyImplicit Equations and Partial Derivatives z = p 1 x2 y2 gives z = f (x, y) explicitly x2 y2 z2 = 1 gives z in terms of x and y implicitly For each x, y, one can solve for the value(s) of z where it holds sin(xyz) = x 2y 3z cannot be solved explicitly for z Prof Tesler 31 Iterated Partial Derivatives Math C / Fall 18 14 / 19

Ocw Aprende Org Resources Res 18 001 Calculus Online Textbook Spring 05 Textbook Mitres 18 001 Strang 13 Pdf

Solved Determine The Second Partial Derivatives Of F X Y Z Tan 5 2x2y4z2 Xx 4y42 8x2y422tan 2x2y422 5 1 Sec 2x2y4 2 5 Course Hero

Partial Derivatives and their Applications 265 Solution Given ( )2/2 2 2 22 m Vr r x y z== =mm (1) Here V xx denotes 2nd order partial derivative of V(x, y, z) with respect to x keeping y and z constant Thus ==∂∂ − ∂∂ (, z=,) ( ) ( ) 222 2 2 2 2221 2Steps to use the derivative calculator Enter function you would like to differentiate and pay attention to the syntax checker tooltip which would inform you if the function is misspelled Enter differentiation variable if it is different from the default value Choose degree of differentiation Click 'Compute' buttonVisit http//ilectureonlinecom for more math and science lectures!In this video I will find the 1st and 2nd partial derivative withrespectto x and y of f(

Answered Assume That Z ƒ W W G X Y X Bartleby

1

If you are taking the partial derivative with respect to y, you treat the others as a constant The derivative of a constant is 0, so it becomes 002x (3y^2) You'll notice since the last one is multiplied by Y, you treat it as a constant multiplied by the derivative of the functionPartial derivative of exp(x^2 y^2) Extended Keyboard;By symmetry (interchanging x and y), zy = ;

How To Solve The Partial Differential Equation P 2 Q 2 Npq Quora

Http Www Math Umass Edu Bill M233 Section Guide2 Pdf

Definition of Partial Derivatives Let f(x,y) be a function with two variables If we keep y constant and differentiate f (assuming f is differentiable) with respect to the variable x, using the rules and formulas of differentiation, we obtain what is called the partial derivative of f with respect to x which is denoted by Similarly If we keep x constant and differentiate f (assuming f isCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicFind all second order partial derivatives of the following functions For each partial derivative you calculate, state explicitly which variable is being held constant \displaystyle f (x,y) = x^2y^3 \displaystyle f (x,y) = y\cos (x) \displaystyle g (s,t) = st^3 s^4 How many second order partial derivatives does the function h defined by h

Rules Of Calculus Multivariate

Derivative Calculator With Steps

 Definition Partial Derivatives Let f(x, y) be a function of two variables Then the partial derivative of f with respect to x, written as ∂ f / ∂ x,, or fx, is defined as ∂ f ∂ x = fx(x, y) = lim h → 0f(x h, y) − f(x, y) h The partial derivative of f with respect to y, written as ∂ f / ∂ y, or fy, is defined asLimit as x goes to 0 of (e^x1x)/x^2 Sketch the level curve, find the gradient, and plot the gradient at the point Partial fraction decomposition of 1/ (x^25x6) Solve 2x4=8 Partial Fraction Decomposition of 1/ (x^25x6) Video Example of Sketching a Gradient Vector, and Level Curve{eq}f(x,y)=\frac{1}{\sqrt{x^{2}y^{2}}} {/eq} Partial Derivative The derivative of the composition of two or more variables with respect to one taking other as the constant is known as the partial

Q Tbn And9gcq9arl5ab K Kkztqdma6czzlslnfprp6ljv7o6a18 5qqda4yy Usqp Cau

Compute The Partial Derivatives Z 3x Squareroot Chegg Com

Let's first think about a function of one variable (x) f(x) = x 2 We can find its derivative using the Power Rule f'(x) = 2x But what about a function of two variables (x and y) f(x, y) = x 2 y 3 We can find its partial derivative with respect to x when we treat y as a constant (imagine y is a number like 7 or something) f' x = 2x 0 = 2x For the y derivative of x^y Let x = k, a constant texf(y) = k^y/tex Natural log of both sides gives texln(f(y)) = ln(k^y)/tex texln(f(y)) = yln(k)/tex Differentiating texf'(y)/f(y) = ln(k)/tex texf'(y) = f(y)ln(k)/tex Since texf(y) = k^y/tex, you now have texf'(y) = ln(k)k^y/tex Substituting for x texf_y = ln(x)x^y/texTo apply the implicit function theorem to find the partial derivative of y with respect to x 1 (for example), first take the total differential of F dF = F ydy F x 1 dx 1 F x 2 dx 2 =0 then set all the differentials except the ones in question equal to zero (ie set dx 2 =0)which leaves F ydy F x1 dx 1

Partial Derivative Examples Math Insight

Partial Differential Equations

Prove\\tan^2(x)\sin^2(x)=\tan^2(x)\sin^2(x) \frac{d}{dx}(\frac{3x9}{2x}) (\sin^2(\theta))' \sin(1) \lim _{x\to 0}(x\ln (x)) \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n}PARTIAL DERIVATIVE LINKSImplicit differentiation Partial derivative (i) y cos x = x^2y^2 (ii) e^z = xyz https//youtube/N6TLvbDCOUkLagrange's MultipFind the directional derivative of f(x, y, z) = xy^2z^3 at P(2, 1, 1) in the direction of Q(0, 3, 5) 💬 👋 We're always here Join our Discord to connect with other students 24/7, any time, night or day

Se13e01 01 Gif

Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch17 Pdf

Answer to Evaluate ({partial y}/{partial x})_z if x^2 y^2 w^2 z^2 = 1 and 5x 4y 3w = c^z By signing up, you'll get thousands ofFor a function of two variables z = f(x,y) the partial derivative of f with respect to x is denoted by ∂f ∂x and is obtained by differentiating f(x,y) with respect to x in the usual way but treating the yvariable as if it were a constant Alternative notations for ∂f ∂x are f x(x,y) or f x or ∂z ∂x Example 2By holding y fixed and differentiating with respect to x\text {,} we obtain the firstorder partial derivative of f with respect to x Denoting this partial derivative as f_x\text {,} we have seen that provided this limit exists In the same way, we may obtain a trace by setting, say, x=150 as shown in Figure 102

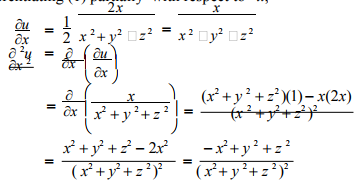
Partial Derivatives Differentiation Business Mathematics Statistics B Com Notes Edurev

3 8 Implicit Differentiation Calculus Volume 1

Therefore at (1,2,4), we get wx = −4, wy = 4, so that the tangent plane is w = 4−4(x −1)4(y −2), or w = −4x 4y x x y 2B2 a) zx = = ; Verify that the function U is a solution for Laplace Equation Verify that the function U = (x^2 y^2 z^2)^ (1/2) is a solution of the threedimensional Laplace equation Uxx Uyy Uzz = 0 From there I saw that for finding the partial derivative Uyy & Uzz I would just have the change the variable being squared in the beginning of the The partial derivative of f with respect to x is fx(x, y, z) = lim h → 0f(x h, y, z) − f(x, y, z) h Similar definitions hold for fy(x, y, z) and fz(x, y, z) By taking partial derivatives of partial derivatives, we can find second partial derivatives of f with respect to z then y

If U Log X 2 Y 2 Xy Then X U X Y U Y Is A 0 B U C 2u Sarthaks Econnect Largest Online Education Community

1 9 3 We Would Like To Make The Length 6 The Only Vectors In The Same Direction As V Are Those Pdf Free Download

4 Partial Derivatives Recall that for a function f(x) of a single variable the derivative of f at x= a f0(a) = lim h!0 f(a h) f(a) h is the instantaneous rate of change of fat a, and is equal to the slope

How To Do Implicit Differentiation 7 Steps With Pictures

The Equation 3y Z 3 3xz Defines Z Implicitly As A Function Of X And Y Evaluate All Three Second Partial Derivatives Of Z With Respect To X And Or Y Verify That Z Is A

Partial Derivative Wikipedia

How To Do Implicit Differentiation 7 Steps With Pictures

Chapter 14 Partial Derivatives Ppt Download

2

Partial Derivatives Calculus 3

100以上 U X 2 Y 2 Z 2 1 2 Partial Derivative 4737

F X Y Z X 2y Y 2z Xz 2 Partial Differential Chegg Com

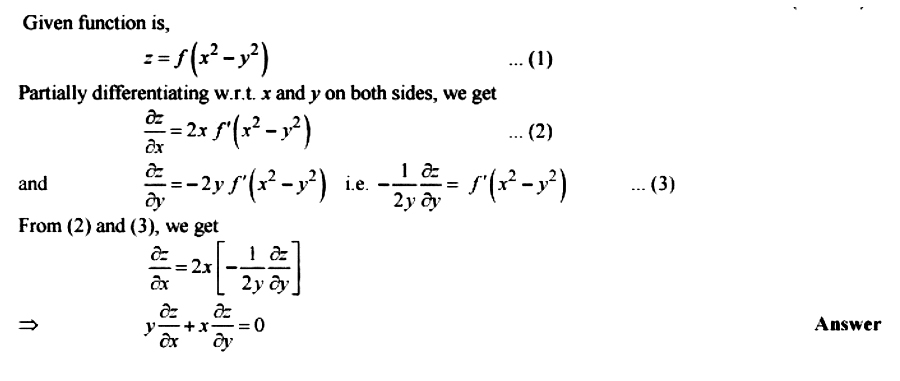
Form A Partial Differential Equation By Eliminating Arbitrary Function From Z F X 2 Y 2 Mathematics 2 Question Answer Collection

1 Given F X Y Z As Z 2 Y Find A The Partial Derivative F X Y Homeworklib

Partial Differential Equation Notes

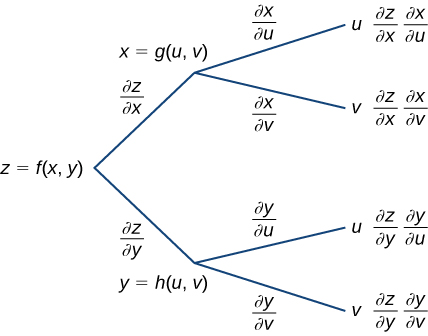
14 5 The Chain Rule For Multivariable Functions Mathematics Libretexts

Lecture Pdf Pdf Partial Differential Equation Tension Physics

Calc 501 1000 By James Bardo Issuu

Answered 7 Find The Second Partial Derivatives Bartleby

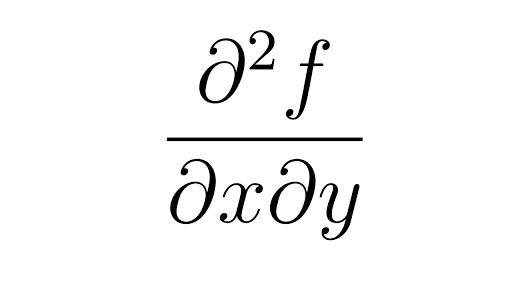
Second Partial Derivatives Article Khan Academy

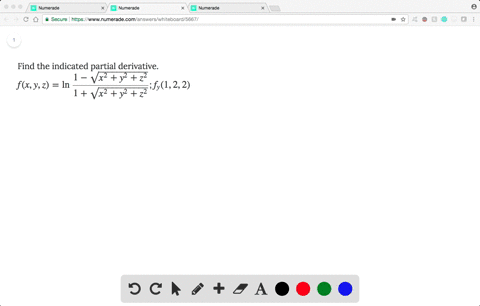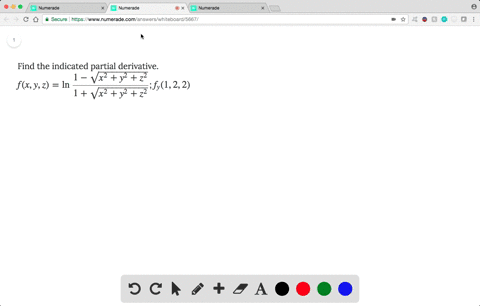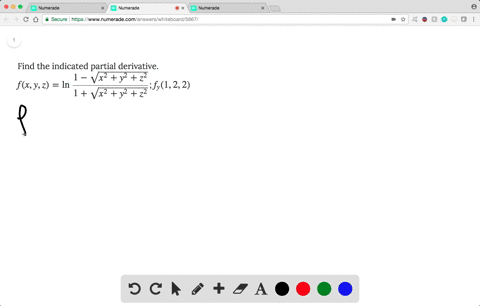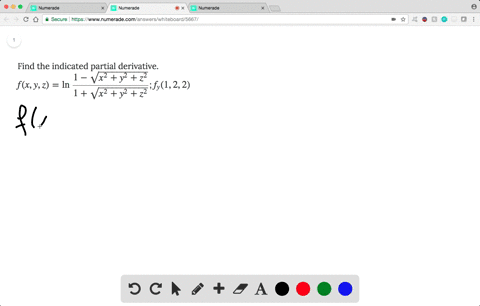
Solved Find The Indicated Partial Derivative F X Y Z Ln Dfrac 1 Sqrt X 2 Y 2 Z 2 1 Sqrt X 2 Y 2

5 Derivative Of The Logarithmic Function

Exercise Partial Derivatives Studocu

Find All The Second Order Partial Derivatives Of The Chegg Com

Ocw Aprende Org Resources Res 18 001 Calculus Online Textbook Spring 05 Textbook Mitres 18 001 Strang 13 Pdf

Partial Derivative Of F X Y Z With Respect To Z Mathematics Stack Exchange

Copyright C Cengage Learning All Rights Reserved 14 Partial Derivatives Ppt Download

Www Whitman Edu Mathematics Multivariable 12 Multivariable 14 Partial Differentiation Pdf

How To Do Implicit Differentiation 7 Steps With Pictures

Calculus Pdf Derivative Differential Topology

2

Partial Differential Equations

Partial Derivatives Introduction Video Khan Academy

Finding Partial Derivatives Implicitly In Exercises Chegg Com

Calculus 3 Partial Derivative 9 Of 30 Find The Partial Derivative Example 5 Youtube

Www Ucl Ac Uk Ucahjva Multi4 Pdf

14 Partial Derivatives Copyright Cengage Learning All Rights

Partial Derivative Of F X Y Xy X 2 Y 2 With Quotient Rule Youtube

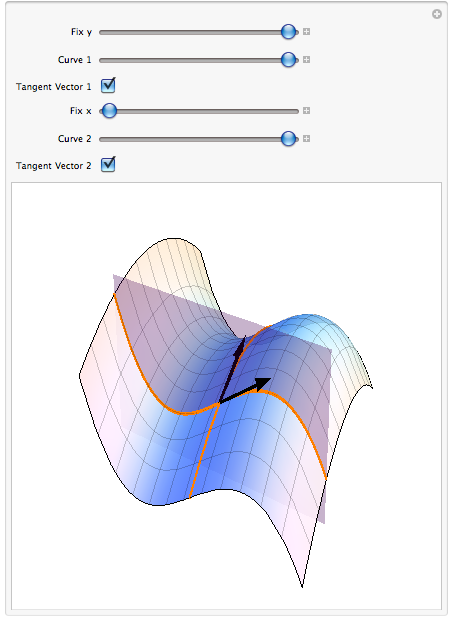
Geometry Of Partial Derivatives

Calculus 3 Partial Derivative 14 Of 30 Find More Partial Derivatives Example 2 Of 2 Youtube

1

1 Pages 1 33 Flip Pdf Download Fliphtml5

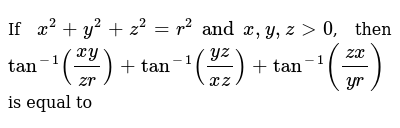
If X 2 Y 2 Z 2 R 2 And X Y Z 0 Then Tan 1 Xy Zr Tan 1 Yz Xz Tan 1 Zx Yr Is Equal To

Partial Derivative Examples Math Insight

If U 2 1 X 2 Y 2 Z 2 Then Show That 2u X 2 2u Y 2 2u Z 2 0 Sarthaks Econnect Largest Online Education Community

How To Eliminate The Arbitrary Function And Hence Obtain The Partial Differential Equation Z X Y F X 2 Y 2 Quora

Multivariate Functions And Partial Derivatives Sage Research Methods

21 Partial Derivatives Problem 4 Most Important Problem Partial Differentiation Youtube

Partial Differentiation And Multiple Integrals Pdf Free Download

Solved Verify That The Function U 1 Sqrt X 2 Y 2 Z 2 Is A Solution Of The Three Dimensional Laplace Equation

2

Calc 501 1000 By James Bardo Issuu

Partial Derivatives Calculus 3

Http Math Depaul Edu Kliechty Math255 Homework Hw06 Solu Pdf

How To Take The Derivative Of This Function Mathematics Stack Exchange

Partial Differentiation And Multiple Integrals Pdf Free Download

Jl Chapter Partial Derivatives 13

Partial Derivatives

Advanced Engineering Mathematics Pages 651 700 Flip Pdf Download Fliphtml5

Find All The First Order Partial Derivatives For The Chegg Com

Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange

Partial Derivative Math Help Forum

Partial Derivatives Boundless Calculus

8 1f U E X Y Z Find D 3 U 2 X Partial Y Partial Z Arcsin E X Y Z Left X 2 Y 2 Z 2 3 X Y Z 1 Right

Problems On Partial Differentiation U Log X 2 Y 2 Z 2 U Tan 1 2xy X 2 Y 2 Z F X Ay Q X Ay Youtube

Www Whitman Edu Mathematics Multivariable 15 Multivariable 14 Partial Differentiation 4up Pdf

Rules Of Calculus Multivariate

Show That W 1 X2 Y2 Z2 Satisfies The Following Chegg Com

Review Of Partial Derivatives Bruce E Shapiro

Homework 14 5

Level Surfaces

Pdf Functions Of Several Variables And Partial Di Erentiation 1 Functions Of Several Variables Mic Mus Academia Edu

Chapter 5 Partial Differentiation

Http Maths Dur Ac Uk Users Daniel Evans Mes Messolutionsupdated Pdf

Question Video The Chain Rule For Multivariate Functions Nagwa

2

Partial Derivatives Archives Www Tinspireapps Com Blog

Www Ualberta Ca Rjia Math214 Hwks Sol8 Pdf

Http Mathweb Math Ncu Edu Tw Calc 98s Assist Hw 98s Hw3 Pdf

2 3 Tangent Plane To A Surface Mathematics Libretexts

Users Math Msu Edu Users Gnagy Teaching 11 Fall Mth234 Mth234 061 E2 F10 Pdf

Incoming Term: partial derivative of 1/(x^2+y^2+z^2), partial derivative of 1/sqrt(x^2+y^2+z^2),